Hi Sean,

In the note you mentioned I did say "Hence the earth's surface curves at approximately 8 inches per mile." I should have said "Hence the earth's surface curves approximately 8 inches in one mile." I will go back and change it. By saying "8 inches per mile" it sounds like it will curve 16 inches in two miles and 4 inches in half a mile but this is not correct. The surface of the earth is a curve and not flat so you can't use ratios. To find the amount it curves in 1 foot you need to perform the the type of calculations in my earlier note.

I reproduced my diagram from the earlier note and added your dimension of 1 foot.

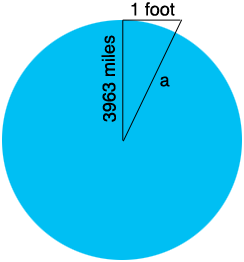
There are 5280 feet in a mile so the radius of the Earth is $3963 \times 5280$ feet and hence Pythagoras Theorem applied to the right triangle in the diagram gives

\[a^2 = (3963 \times 5280)^2 + 1^2 = 20924640^2 + 1^2 \mbox{ square feet.}\]

My calculator gives $a = 20924640.00000002$ feet and hence the Earth curves approximately $0.00000002 \times 12 = 0.00000024$ inches in 1 foot.

Does such a small number make sense? I think so. The Earth curves very slowly and at a distance of one foot the surface would be virtually indistinguishable from a flat plane.

Does the actual value of the number make sense. I think not. The calculations depend of the measurements of 3963 miles and 1 foot being exact. The Earth is not a perfect sphere and I doubt that you can measure 1 foot of glass with the accuracy required.

Harley