Hi Thys,

I found an expression for what you want on the Mechanical Engineering web site at http://www.aboutmech.com/2014/06/equation-of-path-of-projectile.html. It is item number 5. on their page. I don't think however it is in a form that will be particularly useful to you. I redrew the diagram on their site and labeled it to be more consistent with the notation you are using

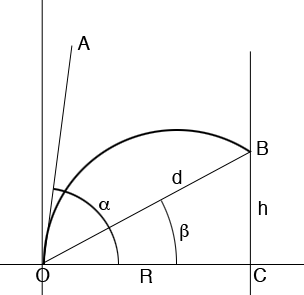
The cannon is at $O,$ the target is at $B,$ $d$ is the distance to the target along the line of sight $OB$ and $h$ is the height of the target above the horizontal. The distances are in feet and the angles are measured in degrees. The line segment $OA$ is in the direction of the initial velocity vector of the cannon ball, at an angle of $\alpha$ degrees to the horizontal. With this notation the formula given on the Mechanical Engineering web site is

\[d = \frac{u^2}{G \; \cos^2 \beta} \left[ \sin[2(\alpha - \beta) - \beta] - \sin \beta\right] = \frac{u^2}{G \; \cos^2 \beta} \left[ \sin[2 \alpha - 3 \beta)] - \sin \beta\right]\]

where $G$ is the force due to gravity ad $u$ is the initial velocity.

Using the facts that

\[\sin(2 \alpha - 3 \beta) = \sin 2 \alpha \cos 3 \beta + \cos 2 \alpha \sin 3 beta\]

\[\sin 3 \beta = 3 \sin \beta - 4 \sin^3 \beta\]

\[\cos 3 \beta = 4 \cos^3 \beta - 3 \cos \beta\]

and reading the values of $\sin \beta$ and $\cos \beta$ from the diagram the expression for $d$ above becomes

\[d = \frac{u^2}{G \frac{R^2}{d^2}} \left[ \left( 4 \frac{R^3}{d^3} - 3 \frac{R}{d} \right) \sin 2 \alpha + \left(3 \frac{h}{d} - 4 \frac{h^3}{d^3}\right) \cos 2 \alpha - \frac{h}{d}\right].\]

Since $R^2 + h^2 = d^2$ this simplifies to

\[1 = \frac{u^2}{G R^2} \left[ \frac{R^3 - 3 R h^2}{R^2 + h^2} \sin 2 \alpha + \frac{3 h R^2 - h^2}{R^2 + h^2} \cos 2 \alpha - h \right] \]

or

\[u = \sqrt{ \frac{G R^2}{\left[ \frac{R^3 - 3 R h^2}{R^2 + h^2} \sin 2 \alpha + \frac{3 h R^2 - h^2}{R^2 + h^2} \cos 2 \alpha - h \right] }} \]

This expression looks onerous but when $h = 0,$ the cannon and the target are at the same altitude it reduces to the expression you sent

\[u = \sqrt{\frac{RG}{\sin 2 \alpha}}.\]

For the example you sent with $\alpha = 45^o$ you have $\sin 2 \alpha = \sin 90^o = 1,$ and $\cos \alpha = \cos 90^o$ so

\[u = \sqrt{ \frac{GR^2 (R^2 + h^2)}{R^3 - 3 R h^2}}\]

I hope this helps,
Harley