Hi Todd,

I drew a sketch of the end of the building, not to scale, and added some lines and labels.

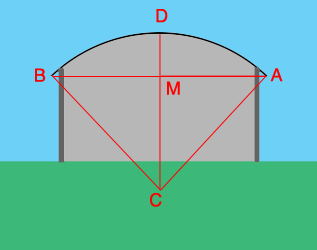
The area of the roof is the length of the arc ADB times the length of the building which is 135 feet. I am assuming that the arc ADB is an arc of a circle. C is the center of the circle and M is the midpoint of the chord AB. The length of the chord ADB is the radius of the circle times the measure of the angle BCA measured in radians.

First let's find the radius $r=|CA|$ of the circle. The triangle AMC is a right triangle with sides of length $|AM| = \large \frac{63}{2} \normalsize = 31.5$ feet, $|MC| = |DC| - |DM| = r - 9.25$ feet and a hypotenuse of length $r$ feet. Hence from Pythagoras Theorem

\[r^2 = 31.5^2 + (r-9.25)^2 = 31.5^2 + r^2 - 18.5 r + 85.56. \]

Solving for $r$ gives $r = 58.26$ feet.

The sine of the angle MCA is $\large \frac{|AM|}{|CA|} = \frac{31.5}{58.26} \normalsize = 0.5407$ and using the inverse sine function on my calculator I get that the measure of the angle MCA is 0.5712 radians. Hence the measure of the angle BCA is $2 \times 0.5712 = 1.1424$ radians.

Finally the area of the roof is the length of the arc ADB times the length of the building which is

\[ 58.26 \times 1.1424 \times 135 = 8986 \mbox{ square feet.}\]

I hope this helps,
Harley