So I've gotten this far:

\[\frac{\mbox{delta(y)}}{\mbox{delta(x)}} = \frac{\cot\left(\frac{7 \pi}{4}\right)-\cot\left(\frac{5 \pi}{4}\right)}{\frac{7 \pi}{4} - \frac{5 \pi}{4}}\]

I'm working through the example with the software, so I'm supposed to simplify the numerator.
I got this:

\[\frac{\mbox{delta(y)}}{\mbox{delta(x)}} = \frac{\cot\left(\frac{7 \pi}{4}\right)-\cot\left(\frac{5 \pi}{4}\right)}{\frac{7 \pi}{4} - \frac{5 \pi}{4}} =\frac{ \cot\left(\frac{\pi}{2}\right)}{\frac{\pi}{2}} = \frac{-1/2}{\pi/2}\]

But they have:

\[\frac{\mbox{delta(y)}}{\mbox{delta(x)}} = \frac{-2}{\pi/2}\]

And I have no idea how they got it. Can you help me?

Hi Brianna,

The problem is that

\[\cot(A) - \cot(B) \neq \cot(A - B).\]

You need to think about $\cot(7 \pi/2)$ and $\cot(5 \pi/2)$ separately. I would do so using a circle diagram.

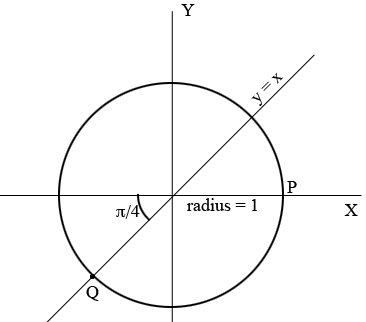
Since $\frac{5}{4} = 1 /frac{1}{4}$ the counterclockwise angle from the positive X-axis to the line segment joining the center of the circle and $Q$ measures $\frac{5 \pi}{4}$ radians. From the diagram what do you know about the sine and cosine of this angle? What is the cotangent of this angle?

Draw the angle which measures $\frac{5 \pi}{4}$ radians on this diagram and ask the same questions.

I hope this helps,
Penny