Hi Bruce,

I am not sure what measurement you want. I assume by a 24 foot pool you mean that the circular pool is 24 feet around. Do you want the distance across the pool, what I have called the diameter in the diagram below,

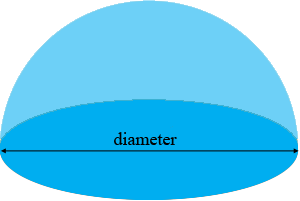
or do you want the distance measured over the top of the dome?

Penny

Bruce wrote back.

I need the length of over the dome. The center pipe of dome goes from one side straight across to other side. How long is center pole of dome

Bruce,

The circumference of your pool is 24 feet and the circumference of a circle is $\pi$ times the diameter $d$ where $\pi$ is approximately 3.1416. Thus for your pool

\[24 = \pi \times d\]

and thus

\[d = \frac{24}{\pi} \mbox{ feet.} \]

Below is a cross-section of the dome. $P$ is the center of the sphere that forms the dome and $r$ is the radius of the sphere.

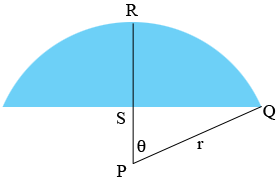
The distance from $S$ to $R$ is 3 feet, the distance from $P$ to $S$ is $r - 3$ feet, and the distance from $S$ to $Q$ is half the diameter and hence this distance is

\[\frac12 \times \frac{24}{\pi} = \frac{12}{\pi}= 3.8197 \mbox{ feet.}\]

Triangle $PQS$ is a right triangle and hence Pythagoras Theorem gives

\[r^2 = 3.8197^2 + (r - 3)^2 = 3.8197^2 + r^2 + 6r + 9.\]

Solving for $r$ gives $r = 3.9317$ feet.

If $\theta$ is the measure of the angle $SPQ$ measured in radians then the length of the arc of the dome from $Q$ to $R$ is given by $r \times \theta.$ To find the measure of the angle $\theta$ you can use

\[\cos(\theta) = \frac{|PS|}{r} =\frac{r - 3}{r} = \frac{0.9317}{3.9317} = 0.2370\]

Using the $\cos^{-1}$ button on my calculator and making sure I am in the radian mode and not the degree mode I get

\[\theta = 1.3315 \mbox{ radians.}\]

Thus the the length of the arc from $Q$ to $R$ is $r \times \theta = 3.9317 \times 1.3315 = 5.2352$ feet. Finally the length of the center pole over the dome is $2 \times 5.2352 = 10.4705$ feet.

I hope this helps,
Penny

Bruce wrote back and indicated that it is the diameter of the pool that measures 24 feet, not the circumference.

If the diameter is 24 feet then the length of $QS$ in the diagram above is 12 feet and in this case Pythagoras theorem gives

\[r^2 = 12^2 + (r - 3)^2 = 144 + r^2 + 6r + 9.\]

and solving for $r$ gives $r = 25.5$ feet.

Now

\[\cos(\theta) = \frac{|PS|}{r} =\frac{r - 3}{r} = \frac{22.5}{25.5} = 0.8824\]

and

\[\theta = 0.4900 \mbox{ radians.}\]

Thus the the length of the arc from $Q$ to $R$ is $r \times \theta = 25.5 \times 0.4900 = 12.494$ feet. Finally the length of the center pole over the dome is $2 \times 12.494 = 25$ feet.