Hi Chris,

If you cut a triangle off each corner to form a regular octagon then my diagram would be

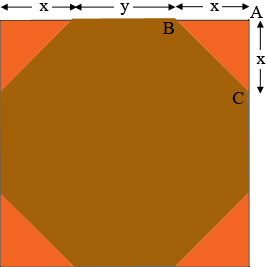
You don't know the lengths $x$ or $y$ but you do know that $x + y + x = 30$ inches.

The key step here is Pythagoras' Theorem. The triangle $ABC$ is a right triangle so Pythagoras' Theorem saya that the length of the side $BC$, $|BC|$ is given by

\[|BC|^2 = |CA|^2 + |AB|^2 = x^2 + x^2 = 2x^2.\]

But $|BC| = y$ so, since $x + y + x = 30$ we know that

\[x + \sqrt{2 x^2} + x = 30 \mbox{ or } x + \sqrt{2} x + x = 30\]

or

\[x = \frac{30}{2 + \sqrt{2}} = 8.79 \mbox{ inches.}\]

I hope this helps,
Penny