Hi Emilie,

I copied the diagram from our response to a similar question and labeled two additional points.

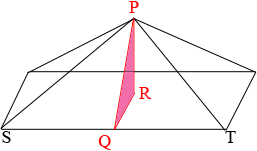
This pyramid has a rectangular base where yours has a regular hexagon as its base but I am interested in $PST$ a triangular part of the surface. The surface area of your pyramid is made up of 6 such triangles and the hexagonal base. You can find the area of a regular hexagon using Stephen's approach.

To determine the area of the triangle $PST$ you need the length of the base $ST$ which you know and the height which is the length of $PQ.$ I am not sure what you mean by the slant height. If is is the length of $PQ$ then you have all the information you need. If the slant height is the length of $PS$ then since $Q$ is the midpoint of $ST$ the triangle $PSQ$ is a right triangle you can use Pythagoras Theorem to find the length of $PQ.$

I hope this helps,
Penny