Hi Gerry,

I think there is something wrong with your question. First I assumed the arc at the top of the window is an arc of a circle. Since $138 \times 12 = 1656$ and $\large \frac{9}{16} = 0.5625$ the radius of the circle is 1656.5625 inches. Here is my diagram of what you described, All the dimensions are in inches. My diagram is not to scale.

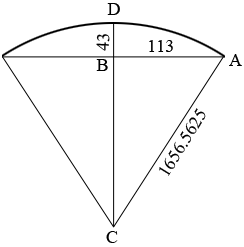
Since the triangle $ABC$ is a right triangle I can use Pythagoras' Theorem to conclude that

\[|BC|^2 = |CA|^2 - |AB|^2 = 1656.5625^2 - 113^2 = 2731430.3164\]

so

\[|BC| = 1652.7039 \mbox{ inches.}\]

But this would mean that $|BD|,$ the rise at the center of the cord is $ 1656.5625 - 1652.7039 = 3.85$ inches rather than 43 inches.

I am not sure what is wrong but how do you know that the radius of the circle is 138' 0 9/16"?

Penny