| |||
| Math Central | Quandaries & Queries |
|
Question from Jeff: Greetings, I came across a question from a textbook from years ago. I've been trying to solve it, but am not sure if my approach is correct. There are 2 squares (1 inner, 1 outer) & 1 circle. The inner square is the largest square that will fit inside the circle. It has an area of 1 unit. The circle is the biggest that will fit in the outer square. What is the area of the outer square? |
Hi Jeff,
I drew a diagram.
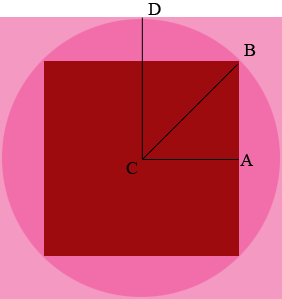
Since the area of the smaller square is 1 square unit each of its sides has length 1 unit. $C$ is the centre of the circle and hence $|CA| = |AB| = \frac12$ units. Use Pythagoras' Theorem to find the length of $CB.$ Since $CB$ and $CD$ are both radii of the circle $|CD| = |CB|.$ But $|CD|$ is half the length of a side of the larges square? What is the length of a side of the larger square? What is its area?
I was surprised by the answer,
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.