Hi Jesse,

I drew a sketch of your pyramid. $R$ is the midpoint of the side $AB$ and $Q$ is at the centre of the square base.

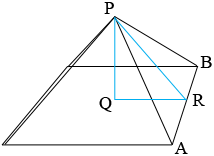
If this is a regular pyramid which I expect it is then the triangle $PQR$ is a right triangle. The length of $QR$ is 15" the length of $PQ$ is 18.25 inches and hence, from Pythagoras' Theorem

\[|RP|^2 = |PQ|^2 + |QR|^2 = 18.25^2 + 15^2 = 558.0625 \mbox{ square inches }\]

and hence $|RP| = \sqrt{558.0625} = 23.62$ inches.

The side $ABP$ of the pyramid is an isosceles triangle and $R$ is the midpoint of $AB$ and hence triangle $RBP$ is a right triangle and Pythagoras' Theorem again gives is

\[|BP|^2 = |PR|^2 + |RB|^2 = 23.62^2 + 15^2 = 783.06 \mbox{ square inches }\]

an thus $|BP| = \sqrt{783.06} = 27.98$ inches.

Again triangle $RBP$ is a right triangle, $|RP| = 15", |PR| = 23.62"$ and hence the measure of the angle $RBP$ is

\[\cos^{-1} \left(\frac{15}{23.62}\right) = 57.58^{o}.\]

I hope this helps,
Penny