| |||
| Math Central | Quandaries & Queries |
|
Question from Joel: Find a formula to calculate the circumferences of an inverted bowl at various heights. E.g. Take an inverted bowl with a diameter of "x" cm and a depth / height of "y" cm. How can I calculate the circumferences at distances of various heights above the base? Alternately, what would be the formula to calculate the distance of the line segment resulting from a line which intersects both sides of a parabola in which that line is drawn parallel to the tangent of the vertex of the parabola at any given distance from the vertex? |
Hi Joel,
Here is my diagram of your inverted bowl. The cross section in the XY-plane is a parabola opening downwards so its equation is
\[y = a x^2 + b\]
where $a$ and $b$ are real numbers.
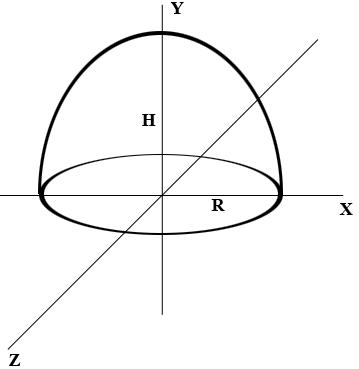
I have made the height of the bowl $H$ cm and the radius of the case $R$ cm. Hence in the XY-plane $(0, H)$ and $(R, 0)$ are on the parabola and hence $b = H$ and $a = - \large \frac{H}{R^2}$ and thus the equation of the parabola is
\[y = - \frac{H}{R^2} x^2 + H.\]
Now suppose you slice the bowl by a plane which is $h$ cm above the base to obtain a circle of radius $r$ cm.
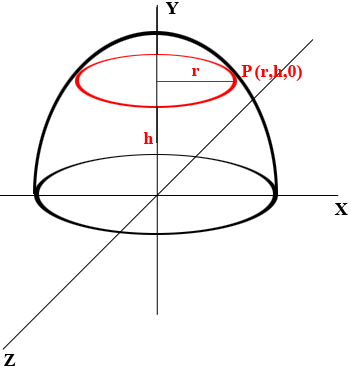
The point $(r, h)$ in the XY-plane is on the parabola and hence
\[h= - \frac{H}{R^2} r^2 + H.\]
Solving for $r$ yields
\[r = \sqrt{\frac{H-h}{H}} R.\]
Using $r$ you can calculate the circumference of the red circle in the diagram above.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.