Hi Katherine,

I hope I am reading this properly. I think you have a 10 foot by 10 foot space that you plan to cover with cinder blocks, packed tightly together and sitting with the void spaces upwards as in the image below. You then plan to fill the void spaces with concrete and you want to know how much concrete you need.

I can't do this without knowing the dimensions of the various parts of the block and how the blocks will be cut to fit the 10 foot by 10 foot space, but I can show you a way to approximate the amount of concrete you will need.

Her is another view of a block, lying on its side. It is $L$ inches long and $W$ inches wide.

I want to see the top of the block, which is facing you at the moment, divided approximately into 5 rectangles.

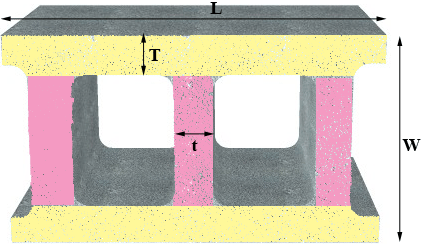
The two yellow rectangles are $L$ inches long and $T$ inches wide and the three pink rectangles are $W - 2T$ inches long and $t$ inches wide.

The area of the rectangular region that the block covers is $L \times W$ square inches and the area of the top of the block that is concrete is $2 \times T \times L + 3 \times (W-2T) \times t$ square inches. Hence the fraction of the top surface of the block that is concrete is

\[\frac{2 \times T \times L + 3 \times (W-2T) \times t}{L \times W}\]

and the fraction of the top of the block that is above void spaces is

\[f = 1 - \frac{2 \times T \times L + 3 \times (W-2T) \times t}{L \times W}.\]

From a block measure $L, W, T$ and $t$ and calculate $f.$

Measure the height $H$ of a block in inches, I think it is the same measurement as $W.$ The area of the dance floor is 120 inches by 120 inches so the volume to be filled with concrete, both from the blocks and the concrete you pour is $120 \times 120 \times H$ cubic inches. The fraction of this which will be filled by concrete your pour is $f$ and hence you will need approximately

\[f \times 120 \times 120 \times H \mbox{ cubic inches.}\]

Since there are 36 inches in a yard to convert this volume to cubic yards divide by $36 \times 36 \times 36 = 46,656.

Penny