Hi Kathryn,

I drew a diagram of the trough at some time $t$ minutes. $D$ is the midpoint of $BC.$ The depth of the water it this time is $h(t) = |AE|$ m.

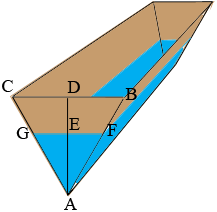
The volume of water in the trough at this time, $V(t)$ is the area of the triangle $FGA$ times the length of the trough which is 6 m. The area of the triangle $FGA$ is $\large \frac12 \normalsize |FG| \times h(t).$ The next task is to find the length $|FG|.$

Triangle $ABC$ is an equilateral triangle with side length 1 m and using the fact that triangle $ABD$ is a 30-60-90 triangle we can see that $|DA| = \large \frac{\sqrt{3}}{2}.$ Also triangles $ABC$ and $AFG$ are similar and hence

\[\frac{|FG|}{h(t)} = \frac{|BC|}{|DA|} =\frac{1}{\frac{\sqrt{3}}{2}}.\]

Thus

\[|FG| = \frac{2}{\sqrt{3}} h(t).\]

Finally you can now write $V(t)$ in terms of $h(t)$ and then differentiating both sides with respect to $t$ gives an equation involving $V^{\prime}(t), h^{\prime}(t),$ and $h(t).$ Evaluating this expression at the time when $h(t) = 0.2$ m gives what you need.

Penny