Hi Kathy,

You didn't give any instructions. Are you to solve for $x?$ If so then the best you can do is approximate a solution.

I am going to let

\[L(x) =2^x \mbox{ and } R(x) = -2x-11\]

and then you are looking for the value of $x$ so that $L(x) = R(x).$

I made a quick sketch of $y = L(x)$ and $y = R(x)$ on the same graph and this was he result

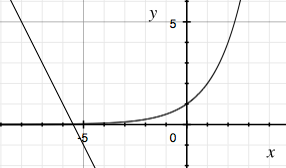
and you can see that where the line $y = R(x)$ crosses the x-axis it is very close to intersecting the curve $y = L(x).$ $R(-5.5) = 0$ and hence the line $y = R(x)$ crosses the x-axis at $(-5.5,0).$ Also $L(-5.5) = 2^-5.5 = 0.0221$ and hence when $x = -5.5$ the expressions $2^x \mbox{ and } -2x - 11$ are almost equal. From the graph you can see that the point where the curves intersect is a little to the left of $x = -5.5$ and hence if you want a better approximation you can try a value of $x$ a little less than -5.5.

If this is for a calculus class you can use the Newton Raphson method to obtain an approximate solution.

I hope this helps,
Penny