| |||
| Math Central | Quandaries & Queries |
|
Question from Kenneth: Hello, I have a question for you. I have a special needs daughter and I want to install a ceiling fan into her room. The fan is 42 inches in diameter. I would like to build a wooden hexagon enclosure to protect the fan. I would like the enclosure to be at least 2 inches wider than the fan on each side measuring from flat surface across to flat surface. How do I figure out the length of each panel so that I can miter them and assemble it? Thank you for your time. |
Hi Kenneth,
Consider regular hexagon and join the opposite vertices to subdivide the hexagon into 6 congruent triangles.
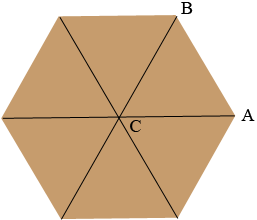
The measure of the angle $BCA$ is $\large \frac{360}{6} \normalsize = 60$ degrees. By the symmetry of the diagram the lengths of $BC$ and $CA$ are equal and the measures of the angles $ABC$ and $CAB$ are equal. Since the sum of the measures of the angles of a triangle is 180 degrees the measure of the angle $ABC$ is 60 degrees.
I redrew the triangle $ABC$ and added $M,$ the midpoint of $AC.$
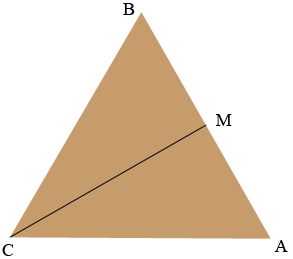
Again by the symmetry angle $CMB$ is a right angle. You want $|CM|$ to be half the diameter of the fan plus 2 inches and hence $|MC| = 23$ inches. Finally
\[\tan(MBC) = \tan\left(60^o \right) = \sqrt{3} = \frac{|CM|}{|MB|} = \frac{23}{|MB|}\]
and hence
\[|MB| = \frac{23}{ \sqrt{3}} = 13.28 \mbox{ inches}\]
and thus $|AB| = 26.56$ inches.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.