Hi Lava,

For this and many other problems in trigonometry it helps to define the sine and cosine in terms of the unit circle rather than by using a right angled triangle.

Draw the unit circle (circle with radius 1) and center at the origin $O.$ Let $OB$ be a line segment for $O$ making an angle of $t$ units and intersecting the unit circle at $B.$ I am going to use radians as the angle units but you can use degrees if you prefer. I am going to define $\cos(t)$ as the X-coordinate of $B$ and $\sin(t)$ as the Y-coordinate of $B.$I then drew a line segment $BA$ from $B$ to intersect the X-axis at $A$ and such that angle $OAB$ is a right angle. Remembering that the circle is a unit circle and hence $|OB| = 1$ you can use the right triangle $OAB$ to verify that my definition os sine and cosine agree with the definition of these functions using a right triangle

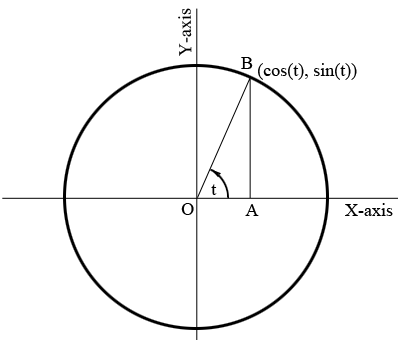
I have drawn my diagram so that $B$ is in the first quadrant. If $t$ is such that $B$ is in the second quadrant hen the X-coordinate of $B$ is negative and the Y-coordinate is positive and hence the cosine of $t$ is negative and the sine of $t$ is positive. You should check that in each quadrant my definition of sine and cosine using the circle is equivalent to the definitions using a right triangle. Finally, what is $t$ is negative? That just means that you measure the angle clockwise from the positive X-axis.

This may seem like a lot of work but seeing sine and cosine this way makes many problems in trigonometry quite easy. For example with your problem to solve $\cos(2x) = 1$ completely. The cosine is the X-coordinate of a point on the unit circle. Since the only point on the unit circle with X-coordinate 1 is $(1,0)$ one solution is $2x=0.$ but you might measure the angle from the positive X-axis going completely around the circle once to obtain $2x = 2 \pi$ radians ($2x = 360^{o}$). Or you might go around the circle twice e to obtain $2x = 2 \times 2 \pi$ radians or three times to obtain $2x = 3 \times 2 \pi$ radians or continuing $2x = n \times 2 \pi$ radians where $n$ is any positive integer. If you go around the circle clockwise so that the angle measure is negative you can also obtain $2x = -n \times 2 \pi$ radians.

Hence $2x = \pm n \times 2 \pi$ or $x = \pm n \pi$ radians where $n$ is an integer.

I hope this helps,
Penny