Hi Pat,

The diagram you sent shows your plan and some calculations.

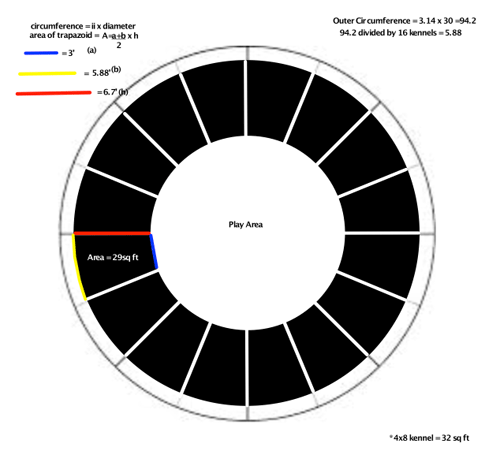
In your calculations you made two assumptions to find the area of a kennel, one is that the blue and yellow lines are straight lines and the other that the length of the red line is the perpendicular distance between the blue and yellow lines. There is nothing wrong with this but I want to show you a way to calculate the area of a kennel without these assumptions.

The area $A$ of a circle of radius $r$ feet is given by $a = \pi \; r^2$ square feet. This the area of interior area of the grain bin is

\[\pi \; \times 15^2 = 706.86 \mbox{ square feet.}\]

The diameter of the play area is $30 - 2 \times 6.7 = 30 - 13.4 = 16.6$ feet and hence its area is

\[\pi \; \times 8.3^2 = 216.42 \mbox{ square feet.}\]

Thus the area of the region containing the kennels is $706.86 - 216.42 = 490.43$ square feet. Since there are 16 kennels the area of each kennel is $\large \frac{490.43}{16} \normalsize = 30.65$ square feet.

To examine the angles I reproduced your diagram and added some orange lines and labels with $C$ at the center of the circle.

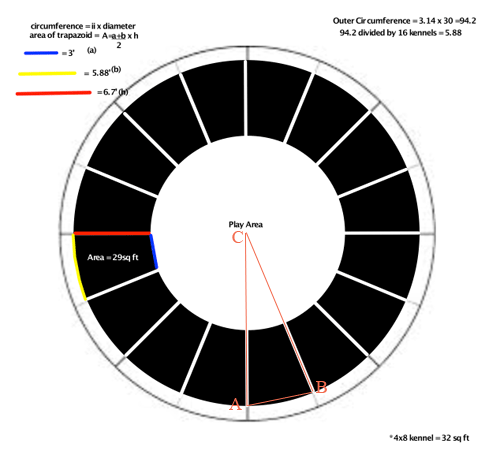
Suppose now that there are $n$ kennels. You can extend the kennel walls to all meet at $C$ and then you have divided the circular disk into $n$ congruent triangles. Hence the measure of the angle $BCA$ is $\large \frac{360}{n}$ degrees.

Write back if you need any further assistance,
Harley