Hi Paul,

I see you attic as composed of two pieces, a rectangular pyramid where the apex of the pyramid is not above the center of the rectangle

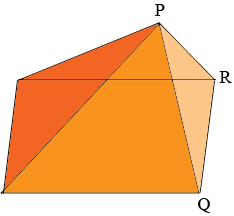
and a dormer $PQRS.$

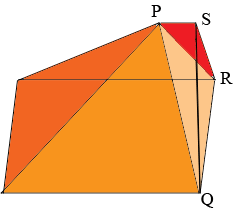
The volume of the attic is the sum of the volumes of the two pieces.The volume of each of these pieces can be calculated from a theorem I have always found surprising.

Suppose $A$ s a region in the plane with an area and $B$ is a point which is $h$ units above the plane. Construct a three dimensional region by drawing a line segment fro $B$ to each point in $A.$ The volume of this region is

\[ \frac13 \times \mbox{ the area of the base A } \times h\]

The rectangular pyramid part of your attic is such three dimensional region. The region $A$ in the plane is a 29 feet by 37 feet rectangle and $h$ is 3.5 feet. Hence the volume of this part of your attic is

\[\frac13 \times (29 \times 27) \times 3.5 \mbox{ cubic feet.}\]

The dormer is also a region whose volume can be calculated in a similar fashion. Think of the triangle $SQR$ as the base and $S$ as the point not in the plane of the base. The height of $S$ above the base plane is the length of $PS.$ The base of the triangle is $QR$ which has length 29 feet and its height, the perpendicular distance from $QR$ to $S$ is 3.5 feet. Hence the area of the triangle $SQR$ is $\large \frac12 \normalsize \times 27 \times 3.5$ square feet. Finally the volume of the dormer is

\[\frac13 \times \left(\frac12 \times 27 \times 3.5 \right) \times 7 \mbox{ cubic feet.}\]

I hope this helps,
Harley