Hi,

Suppose the length of the arc is $a$ units, the radius of the circle is $r$ units and the angle measurement is $t$ degrees as in the diagram.

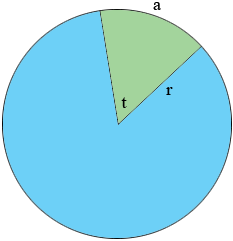
The circumference of the circle is $2 \pi \; r$ units and $a$ the length of the arc is a fraction of the circumference.

The angle measurement all the way around the circle is 360 degrees and the angle measurement $t$ is a fraction of this.

By the symmetry of the circle these two fractions are equal. That is

\[\frac{a}{2 \pi \; r} = \frac{t}{360}.\]

Solving this for $a$ gives the more familiar expression

\[a = 2 \pi \; r \frac{t}{360}.\]

Since you know $a$ and $t$ you can solve for $r.$

If you measure the angle $t$ in radians rather than degrees the expression is simpler. If the angle is measured in radians the expression is

\[ a = r t.\]

I hope this helps,
Penny