Hi Rand,

I drew a diagram, assuming that the arch is parabolic.

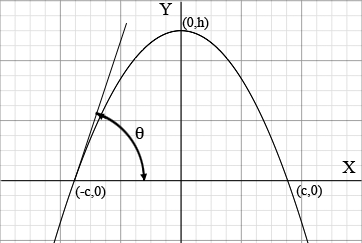
Since the curve is a parabola opening downwards its equation is $y = a - bx^2$ for some positive real numbers $a$ and $b.$ What you know is the height of the arch which I have called $h$ and the measure of the angle $\theta$ and you want to find $2c.$

Using the equation $y = a - bx^2$ and the fact that $(0,h)$ and $(-c,0)$ are on the curve you can deduce that $a = h$ and $h = b c^{2}.$ You now can use the fact that the slope of the tangent to the parabola $y = a - bx^2$ at $x = -p$ is $-2bp$ and that the slope of the slope of the tangent to the parabola $y = a - bx^2$ at $(-c,0)$ is $\tan(\theta)$ to show that $\tan(\theta) = 2bc.$ solve for $c.$

I hope this helps,
Harley

Rand,

After reading your problem again I think that what was expected was a circular arch rather than a parabolic arch. If so my diagram would change to

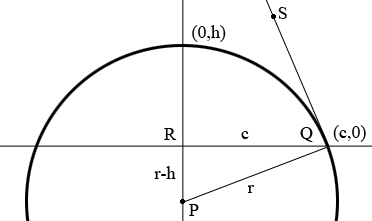
$P$ is the center of the circle. Again $h$ is known and the measure of the angle $SQR$ is known and I am going to call it $\theta$ degrees. Since $SQ$ is tangent to the circle and $PQ$ is a radius of the circle the angle $SQP$ is a right angle and hence the measure of the angle $PQR$ is $90 - \theta$ degrees.

The triangle $PQR$ is a right triangle. What trig function relates the measure of the angle $PQR,$ the length of $RP$ and the length of $PQ?$ Use this to find $r.$ Use another trig function to find $c.$

Harley