Hi Russell,

I'm not sure I understand but here is my diagram. I am taking O.D. to mean outside diameter.

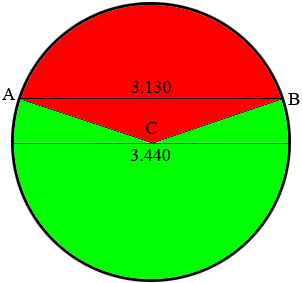
$AB$ is the chord and $C$ is the center of the circle. I have shaded two segments and since you said "largest" I assume you mean the sector I have coloured green. I then took this sector and formed a slab of an unknown thickness.

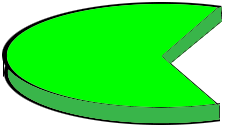
My interpretation is that you want the thickness of this slab o that its volume is 0.1143 cubic inches.

Is this correct? If not can you clarify, perhaps with a diagram.

Penny

Russell replied

Penny Yes you have it correct 2 changes The O.D. is 4.437 and the chord length is 3.034 The vol of .1143 is correct I calculated the area of the segment that needs to be cut as 7.316 " so wouldn't thickness of the slab be thickness = vol (.1143) divided by area (7.316") = .016" thick ? Thanks

I redrew my diagram with the dimensions changed. $C$ is the center of the circle and $D$ is the midpoint of the chord. $\large \frac{4.437}{2} \normalsize = 2.2185$ and $r = \large \frac{3.034}{2} \normalsize = 1.517$ where $r$ is the radius of the circle.

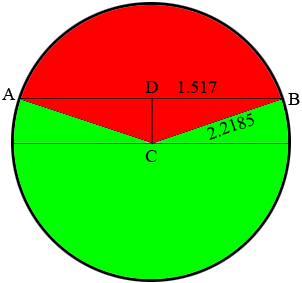
The area of a circle is $\pi\; r^2$ square units thus the area of the circle above is

\[\pi\; \times r^2 = \pi\; \times 2.2185^2 = 15.4621 \mbox{ square inches.}\]

The area of the sector you want, the green sector, is larger than half the area of the circle which is $\large \frac{15.4621}{2} \normalsize = 7.7311$ square inches so your answer of 7.316 square inches is too small. I found the area of the green sector by first finding the area of the red sector and subtracting it from the area of the circle.

Let the measure of the angle $ACB$ be $\theta$ radians then the area of the red sector is $\large \frac12 \normalsize \pi\; r^2 \theta.$ The measure of the angle $DCB$ is $\large \frac{\theta}{2}$ and

\[\sin\left(\frac{\theta}{2}\right) = \frac{1.517}{2.2185} \]

and thus

\[\theta = 2 \times \sin^{-1} \left(\frac{1.517}{2.2185} \right) = 0.93522 \mbox{ radians.}\]

Hence the area of the red sector is

\[\frac12 \times 2.2185^2 \times 0.93522 = 2.3015 \mbox{ square inches.}\]

Finally this gives the area of the green sector as $15.4621 - 2.3015 = 13.1606$ square inches.

Thus the thickness of the slab to give a volume of 0.1143 cubic inches is

\[\frac{0.1143}{13.0606} = 0.0087 \mbox{ inches.}\]

Penny