| |||
| Math Central | Quandaries & Queries |
|
Question from Sal, a student: There is a right isosceles triangle. Inscribed inside of it, is the largest possible circle. I want to find out a way of only using the rules/laws of geometry, or is that not possible. |
Hi Sal,
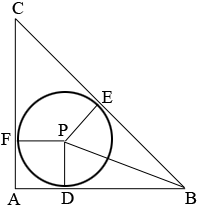
I drew a diagram and labeled some points. $P$ is the centre of the circle and $D, E$ and $F$ are points where the sides of the triangle are tangent to the circle. Thus angles $CAB, PDB$ and $BEP$ are right angles. Suppose the radius of the circle is $r$ and the side length of $CA$ is $s.$ By the symmetry of the diagram $E$ is the midpoint of $BC.$ Notice also that the length of $AD$ is $r.$
I used Pythagoras Theorem 3 times. Once for the triangle $ABC$ to find the length of $BC$ and hence $BE$ in terms of $s.$ A second for triangle $BEP$ to find the length of $BP,$ and a third time for triangle $BPD$ to write an equation involving $s$ and $r.$ Solve for $r.$
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.