Hi Sasha,

I would stat by drawing a graph of $y = x(x-2).$

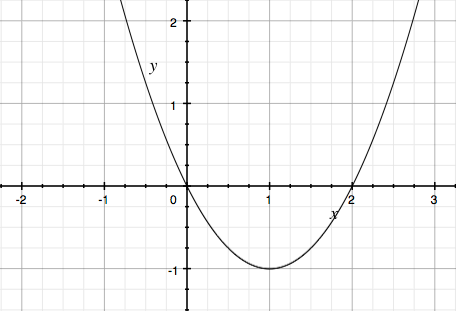
To invert this function graphically you first interchange the roles of $x$ and $y$ by labeling the X-axis as the Y-axis and the Y-axis as the X-axis.

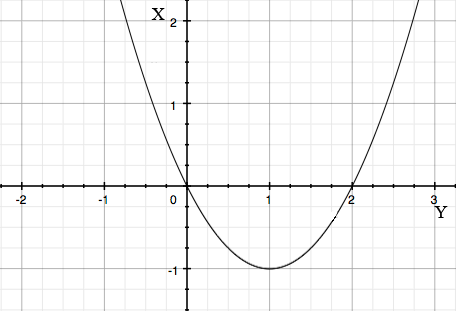
Next flip the graph so that the X-axis is horizontal with positive to the right and the Y-axis vertical with positive upwards.

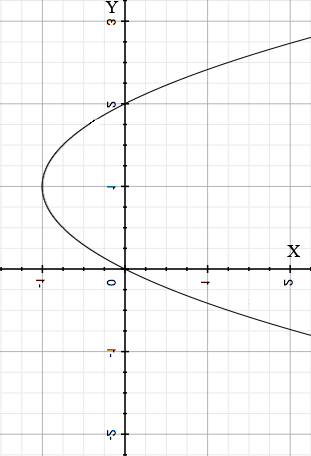
This is a graph of the inverse of $y = x(x-2)$ and you can clearly see why it is not a function. For each $x$ value greater than 1 there are two points on the graph with that $x$ value.

The instruction "Suggest a domain restriction which would ensure that the inverse is a function." means to suggest a domain restriction on the original function $y = x(x-2)$ so that the inverse is a function. For example if you define $y = x(x-2)$ for $x \geq 1$ then the graph of this function is

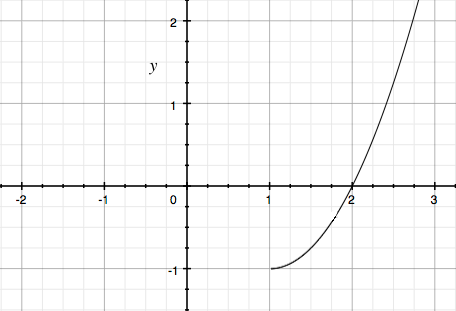
and the inverse of this function is a function.

I hope this helps,
Penny