Hi Tasha,

I drew two diagrams one of the circle and the other of the cone.

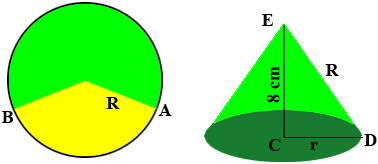
The yellow portion of the circle on the left is cut out and the green portion is rolled up to form the cone. $R$ is the radius of the circle on the left and $r$ is the radius of the circular base of the cone. THe triangle $CDE$ is a right triangle so Pythagoras theorem will give you an equation is $R$ and $r.$ The circumference of the circular base of the cone is $2 \pi \; r$ centimeters and this length is the length of the arc of the circle on the left measured counterclockwise from $A$ to $B.$

The circumference of the circle on the left is $2 \pi \; R$ centimeters and the length of the arc from $A$ to $B$ is a fraction of this length. Since the measure of the angle subtending the counterclockwise arc from $A$ to $B$ measures 216 degrees, the symmetry of the circle guarantees that the length of the arc from $A$ to $B$ is $\large \frac{216}{360} \times$ the circumference of a circle of radius $R.$ This is the circumference of a circle of radius $r$ so

\[2 \pi \; r = \frac{216}{360} \times 2 \pi \; R.\]

Solve this equation for $R,$ substitute into the expression you have for Pythagoras Theorem and solve for $r$

Penny