Hi Yolani,

You didn't send a diagram but I think it looks like this.

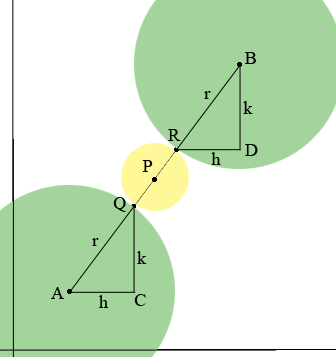
I labeled some points and placed $C$ and $D$ so that $ACQ$ and $RDB$ are right triangles. You said equal circles so by that I assume that the circles with centers $A$ and $B$ have the same radius which I called $r.$

Triangles $ACQ$ and $RDB$ are similar and $|AQ| = r = |RB|$ and hence the triangles are congruent and that $|AC| = |RD|$ and $|CQ| = DB|.$ I called these lengths $h$ and $k.$

Write the coordinates of $Q$ and $R$ in terms of $h$ and $k$ and then you can write the coordinates of $P$ since it must be the midpoint of $QR.$

From this you can see that the coordinates of $P$ do not depend on the value of the radius$r$ so why not make the calculations easier and take $r = 0?$

Penny