Hi Amy,

I want to look at the problem you quote, "If a bright flashlight has a light intensity of 15.0 candela at a distance 1.00 m from the lens, what is the intensity of the flashlight 100.0 m from the lens?" and solve it using a different approach than was used on the SoftSchools site.

They use the variable $I$ for the intensity of light in the units candela and they use the variable $d$ for the distance between the light source and the observer in meters. The statement that "The intensity of light is inversely proportional to the square of the distance." means that there is a constant $C$ so that

\[I = C \times \frac{1}{d^2},\]

where $C$ is in the units candela time meters squared.

The fact that $C$ is a constant means that its value is the same, regardless of the values of $I$ and $d.$

The problem also states that when $I = 15.0$ candela, $d = 1.00 m$ and hence

\[15.0 = C \times \frac{1}{1.00} \mbox{ or } C = 15.0 \mbox{ candela } \times m^{2}.\]

Thus we know that

\[I = 15.0 \times \frac{1}{d^2}.\]

The question then asks for the value of $I$ when $d = 100.0$ m. Substituting into the equation above gives

\[I = 15.0 \times \frac{1}{10000} = 0.0015 \mbox{ candela.}\]

To see how that looks graphically I made the horizontal axis be distance, $d$ in meters and the vertical axis intensity, $I$ in candela and plotted

\[I = 15.0 \times \frac{1}{d^2}.\]

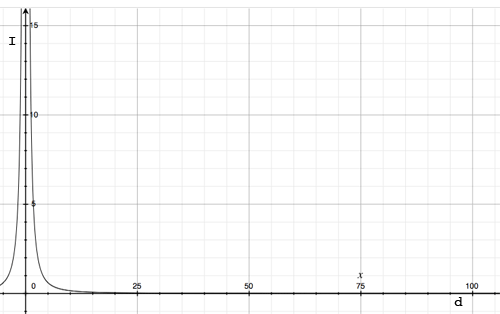
I hope this helps,
Penny