Hi Angelo,

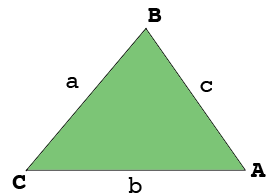
I drew your triangle, not to scale.

The lengths of the sides are $a, b$ and $c$ as labeled, all in centimeters. Let $A$ be the measure of the angle at A in degrees and $C$ the measure of the angle at C in degrees. The side lengths and angle measures are all changing with time so they are all functions of time $t$ in seconds.

You know $b, c $ and $A$ at a particular time, say $t = t_0$ seconds and you also know the rate of change of these quantities at this time. You also Your question asks for the rate of change of the length of the side $AB$ which you already know. I think you are to find the rae of change of the length of the side $BC,$ that is $a$ at this time.

What you need is a mathematical expression involving $a, b, c$ and $A$ which you can differentiate with respect to $t.$ This will then give you an expression involving these three quantities and their derivatives. Five of these quantities you know at time $t_0$ seconds so you can solve for the sixth.

One problem remains, find a mathematical expression involving $a, b, c$ and $A.$Do you know one? Write back if you need more assistance.

Penny