Hi Chuck,

I drew a diagram from my reading of your description. All the dimensions are in inches.

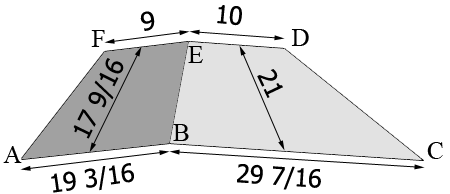
The points $A, B$ and $C$ lie in a base plane and the points $D, E$ and $F$ lie in a top plane parallel to the base plane. The vertical distance between these two planes is 14 1/4 inches.

I redrew the diagram with a few extra points labeled. Imagine that I put a Cartesian coordinate system in the diagram with the origin at $B$, $BC$ on the X-axis, $BA$ on the Y-axis and the Z-axis upwards.

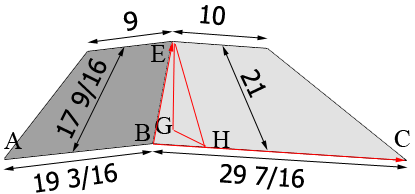
The point $G$ is on the base plane (the XY plane) directly below $B$ and $EH$ is perpendicular to the X-axis. Thus the length of $EH$ is 21 inches and the length of $EG$ is 14.25 inches. The angle $EGH$ is a right angle and hence using Pythagoras Theorem I get the length of $GH$ to be 15.43 inches. This is the Y-coordinate of the point $E.$ In a similar fashion I found that the X-coordinate of $E$ is 10.27 inches. Hence the vector $BE$ can be written $(10.27, 15.43, 14.25).$ The vector $BC$ can also be written $(29 7/16, 0, 0).$

The cross product of the vectors $BC$ and $BE$ gives a vector perpendicular to the plane containing $B, C, D$ and $E$ (the front panel) which can be normalized to length 1 to obtain a unit vector $n_1} perpendicular to the front panel. I used the command

Cross({29 7/16, 0, 0},{10.27, 15.43, 14.25})

in Wolfram Alpha to make this calculation and then normalized the result to obtain

\[n_1 = (0., -0.678458, 0.734639) \]

In a similar fashion I obtained

\[n_2 = (-0.811264, 0., 0.58468)\]

a unit vector perpendicular to the side panel.

Now look at the point $B$ from below.

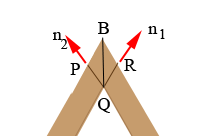
The angle $PQR$ is the angle between $n_1$ and $n_2$ can be found again using Wolfram Alpha with the command

Arccos({-0.811264, 0., 0.58468}.{0., -0.678458, 0.734639})*180/Pi

The result is that the measure of the angle $PQR$ is 64.5623 degrees, and hence the measure of the angle $BQR$ is $\frac{64.5623}{2}= 32.2812$ degrees and the measure of the angle $RBQ$ is $90 - 32.2812 = 57.7186$ degrees.

Harley