Hi Domenick,

I drew two of the seven circles with centers $A$ and $B.$ $C$ is the center of the inscribed and circumscribed circles and $P$ is the point of tangency of the two circles.

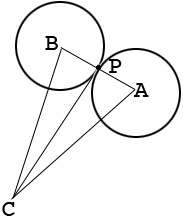
By the symmetry of the diagram with all 7 circles, the measure of the angle $BCA$ is 360/7 degrees. Triangles $APC$ and $PBC$ are congruent, can you see why? Thus angle $APC$ is a right angle. You know that $|AP| = 0.019685$ units. What is the length of the line segment $CA?$

Penny