Hi Doug,

The subject of your email was "Distance between a chord and its arc on a circle" so that is what I'll try to answer. Let me know if this is not what you want.

In my diagram the arc $AB$ is path of the Earth over 7 days and the radius of the circle is 93 million miles. The "Distance between a chord and its arc on a circle" is the length of the line segment $ED.$

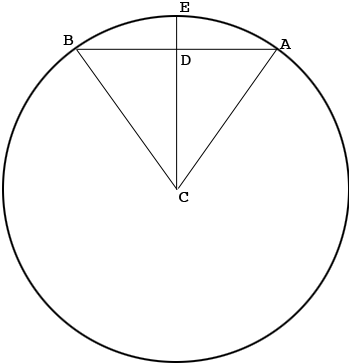
As you pointed out the measure of the angle $BCA$ is $\large \frac{7}{365} \normalsize \times 360^{0} = 6.90^{0}.$ Hence the measure of the angle DCA$ is half of this. The angle $ADC$ is a right angle and thus

\[\cos(DCA) = \frac{|DC|}{|CA|}\]

and hence

\[|DC| = 93,000,000 \times cos\left( \frac{6.90}{2}\right) = 93,000,000 \times 0.998 = 92,831,254 \mbox{ miles.}\]

Thus $|ED| = 93,000,000 - 92,831,254 = 168,746$ miles.

You can't put much faith in this number since the path of the Earth is not a circle and the radius of the "circle" is only approximately 93 million miles.

Penny