Hi Grayson,

I want to show you a way to approach this problem and others like it. I am going to consider the function

\[g(x) = x^4 + 2x^3 - 3x^2\]

and ask for what intervals of the real line is $g(x)$ positive and for what intervals is it negative?

As a first step I want to find all real numbers $x$ for which $g(x) = 0.$ To do this I ned to factor $g(x).$

\[g(x) = x^4 + 2x^3 - 3x^2 = x^2\left(x^2 + 2x - 3\right) = x^2(x-1)(x+3).\]

Hence $g(x) = 0$ at $x = -3, 0$ and $1.$

These three points subdivide the real line into four intervals,

1. minus infinity to minus 3
2. minus 3 to 0
3. 0 to 1, and
4. 1 to plus infinity.

Next select a point in one of these intervals, I am going to select -1 which is in the interval from -3 to 0. $g(-1) = -4$ hence $gx)$ is negative at $x = -1.$ Can there be an $x$ in the interval from -3 to 0? The fact that $g(x)$ is continuous means that the answer is no. This is a consequence of the Intermediate Value Theorem. If $g(a)$ is positive and $g(b)$ is negative then for some $x$ between $a$ and $b, g(x) = 0.$ but $g(x)$ is only 0 at $x = -3,0$ and $1.$ Hence $g(x)$ is negative on the interval from -3 to 0.

Now try a different point in a different interval, say $x = 2$ in the interval from 1 to plus infinity. Is $g(2)$ positive or negative. Whatever sign it has it retains for the entire interval.

Finally look at the remaining two intervals.

To verify your answer here is a graph of $y = g(x).$

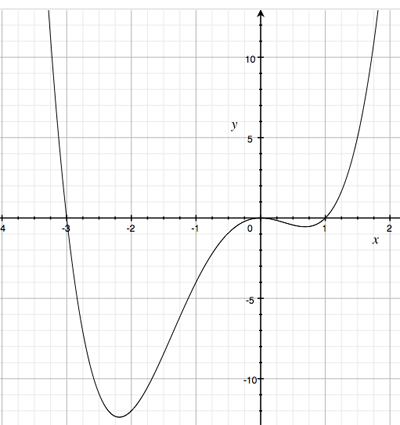
I hope this helps,
Penny