Hi Jessica,

In the circle below of radius 7.5 cm I have cut out a sector with center angle 240 degrees from which I want to construct a cone.

Since $\large \frac{240}{360} \normalsize = \frac{2}{3}$ the symmetry of the circle tells us that the length of the arc forming the green section is two-thirds of the circumference of the circle.

The cone below is formed from the green sector of the circle above.

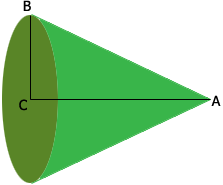
$|AB|,$ sometimes called the slant height of the cone is the radius of the circle above, 7.5 cm. The circle tat forms the base of the cone has a circumference which is the arc formed by the green sector in the first diagram. Since you know the length of this arc and an expression for the circumference of a circle you can calculate the radius, $|BC|$ of the base of the cone.

Finally triangle $ABC$ is a right triangle and you know the lengths of two of its sides you can use Pythagoras Theorem to find the length of the third side, the length of the cone.

Penny