Hi,

I want to think of forming the cone by cutting out the red sector from the circle on the left and using the green sector to form the cone.

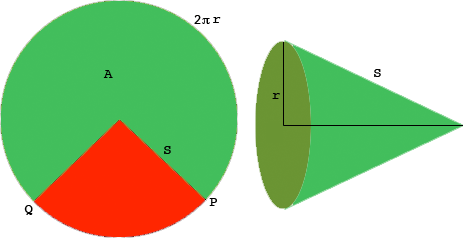
The area of the green sector, $A$ you know as well as the radius $r$ of the circle that forms the base of the cone. You want to determine the slant height $S.$

Since the circumference of the circle that forms the base of the cone comes from the arc of the large circle measured counterclockwise from $P$ to $Q,$ the length of this arc is $2 \pi r.$ The symmetry of the circle tells us that the area of a sector is proportional to the length of the arc that forms the sector. Thus

\[\frac{A}{2 \pi r} = \frac{\mbox{the area of a circle of radius S}}{\mbox{the circumference of a circle of radius S}} = \frac{\pi S^2}{2 \pi S}\]

Simplification gives $A = \pi r S.$

Penny