Hi John,

The surface is composed of 5 pieces, the top, the two ends and the two sides.

The top is a rectangle with width 6 feet and length 1,250 feet so its area is $6 \times 1,250$ square feet.

Each end is a trapezoid

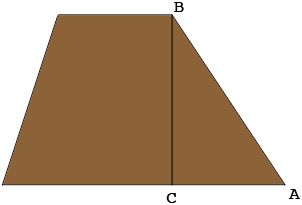
and the area of a trapezoid is the average of the lengths of the parallel sides times the distance between the parallel sides. In your case the average of the lengths of the parallel sides is $\large \frac{6 + 40}{2} \normalsize = 23$ feet so the area of each trapezoidal end is $23 \times 10$ square feet. You have two of these.

What remains is the area of the two sides of the levee, each of which is a rectangle. In my diagram above one of the sides has width the distance between $A$ and $B, |AB|$ feet and length 1,250 feet. Thus its area is $|AB| \times 1,250$ square feet. If you don't know the length $|AB|$ but you know the length $|CA|$ you can use Pythagoras' theorem to find $|AB|.$ Triangle $ABC$ is a right triangle so Pythagoras' theorem tells that

\[|BC|^2 + |CA|^2 = |AB|^{2}.\]

You know that $|BC| = 10$ feet so

\[|AB| = \sqrt{100 + |CA|^2} \mbox{ feet.}\]

You can calculate the area of the second side of the levee in a similar fashion.

I hope this helps. Write back if you need more assistance.

Penny