Hi Kristin,

The important measurement is the length of the fighter's arm. In my diagram $S$ is his shoulder and $F$ is the fist at the end of his arm.

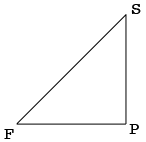
I drew a horizontal line from $F$ and a vertical line from $S$ to meet at a point $P.$ The distance from $S$ to $F$ is the length of the fighter's arm which I will cal $a.$ The distance from $F$ to $P,$ which I will call $d$ is the distance between the two men. The measure of angle $PSF$ is $45^o$ and hence the measure of the angle $SFP$ is also $45^o.$ The triangle $SFP$ is thus an isosceles triangle and the length of the side $PS$ is therefore $d.$

Triangle $SFP$ is a right triangle and hence Pythagoras Theorem tells us that

\[d^2 + d^2 = a^2 \mbox{ or } d^2 = \frac{a^2}{2}\]

Thus the distance between the two men is

\[d = \frac{a}{\sqrt{2}}\]

I hope this helps,
Penny