Hi Lola,

I started by plotting the curve $y = 2 \sqrt{x}$ and then the line with $C=0,$ that is $y = x.$

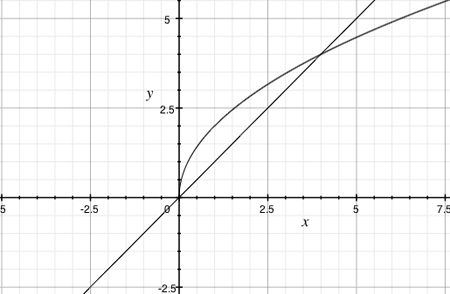
Clearly $y = 2 \sqrt{x}$ and $y = x$ intersect at $x = 0$ and, from the graph, at some other point also.

The line $y = x + C$ is parallel to $y = x.$ If $C$ is negative $y = x + C$ is below the line $y = x$ and will only intersect the curve once. From the graph, if $C$ is slightly larger than zero the line will intersect the curve twice. Again from the graph it looks like for some value of $C$ the line will be tangent to the curve and intersect the curve exactly once. If $C$ is too large then $y = x + C$ will miss the curve entirely.

To determine where the line $y = x + C$ and the curve $y = 2 \sqrt{x}$ intersect you need to solve

\[2 \sqrt{x} = x + C.\]

I would square both sides and simplify to obtain a quadratic in $x.$ A quadratic equation has two distinct roots if and only if the discriminant is positive. Find the discriminant of your equation and determine for what values of $C$ it is positive.

Does your answer agree with the graphical development I gave above?

Penny