Hi Mandy,

I drew a graph of $y = 4x - 5x^2 = x(4 - 5x)$ and a line through the origin that looks like it divides the area between the graph and the X-axis in half. This line intersects the graph at the origin and Q which has coordinates $(a,b).$ This line then has slope $\large \frac{b}{a}.$

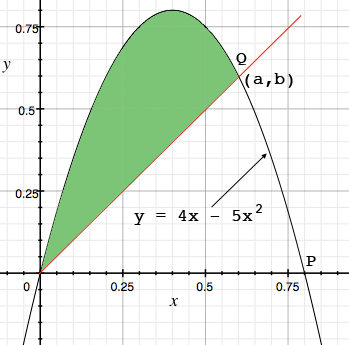
I would first integrate $ y = 4x - 5x^2$ from $0$ to $P$ to find the area between the graph and the X-axis. Call this area $B.$

Next find the area shaded green in the diagram, again by integration. Set this area equal to $\large \frac{B}{2}$ and solve for $a.$

Write back if you need more assistance,
Penny