Hi Mike,

The volume of the berm is the area of the cross section times the length of 700 feet. I have drawn a sketch of the cross section, not to scale.

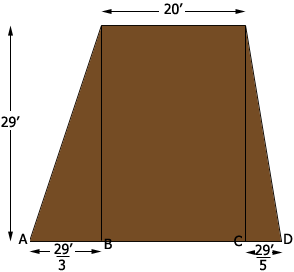
On the left the slope is 3-1 so the height is 3 times the distance from $a$ to $B.$ thus the distance from $A$ to $B$ is $\large \frac{29}{3} \normalsize = 9.67$ feet. On the right side the height is 5 times the distance from $C$ to $D$ so the distance from $C$ to $D$ is $5.8$ feet.

The shape of the cross section is called a trapezoid and the area of a trapezoid is (the average of the lengths of the parallel sides) times (the distance between the parallel sides). Thus the area of your trapezoid is

\[\frac{20 + (20 + 9.67 + 5.8)}{2} \times 29 = 804.32 \mbox{ square feet.}\]

Hence the volume of the berm is $804.32 \times 700 = 563,020.5$ cubic feet.

There are 3 feet in a yard and hence $3 \times 3 \times 3 = 27$ cubic feet in a cubic yard so you can divide the volume in cubic feet by 27 to obtain the volume in cubic yards. Alternatively you could just ask Google by typing What is 563020.5 cubic feet in cubic yards into the Google search window.

Penny