HI Naveen,

I drew a piece of the polygon and its inscribed circle.

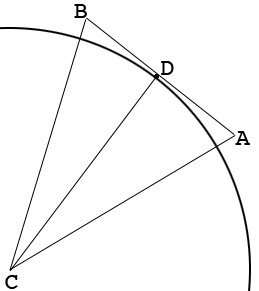
$AB$ is one side of the polygon, $C$ is the center of the circle and $D$ is the point on $AB$ where $AB$ is tangent to $CD.$ Since $AB$ is tangent to the circle and $CD$ is a radius, the angle $ADC$ is a right angle. Since the polygon is regular and has $n$ sides the measure of the angle $BCA$ is $\large \frac{360}{n}$ degrees. Can you show that $D$ is the midpoint of $AB?$ What is the measure of the angle $DCA?$ What trig function relates the measure of the angle $DCA$ to the lengths of $AD$ and $DC?$

Penny