| |||
| Math Central | Quandaries & Queries |
|
Question from Paulina: Find the rate of change of the distance between the origin and a moving point on the graph of y=x^2 +1 if dx/dt=2 centimeters per second |
Hi Paulina,
Let $P(x, y)$ be a point on the graph of $y = x^2 + 1$, let $O$ be the origin and $Q$ the point $(x, 0).$
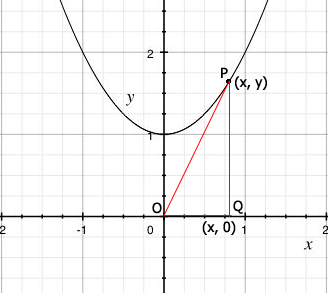
Since $P$ is on the graph we know that $y = x^2 + 1$ and hence the distance from $Q$ to $P$ is $y = x^2 + 1.$ Use Pythagoras Theorem to write $D$ the distance from $O$ to $P$ as a function of $x.$ Differentiate $D$ with respect to $t.$
Penny
 |
||
| * Registered trade mark of Imperial Oil Limited. Used under license. | ||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.