Hi Roberto,

What I see is this

where each of the long sides is 20 feet long and the measure of each of the internal angles is 135 degrees.If this is correct then I need more information to determine the lengths of the six shorter sides. In particular do you know the distance between the long sides?

Penny

Roberto wrote back.

I was hoping to divide two twenty foot sticks into three equal lengths of 6.67', using the 135 degree fittings, so I honestly don't know what the distance would be between long sides.

Sides of length 6.67' will certainly work, I just thought that the width of the "ring" might be important. Once you know one you can determine the other.

Suppose $d$ is the distance between the long sides as in the diagram below and $x$ is the lengths of the short sides.

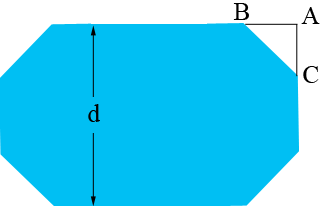
The triangle $ABC$ is an isosceles right triangle with the length of the hypotenuse $x$ feet and thus Pythagoras Theorem says that the length of $AC$ is $\frac{x}{\sqrt 2}$ feet. Thus

\[d = 2 \times |AC| + x = \sqrt 2 x + x = \left(1 + \sqrt 2 \right) x.\]

Hence if $x = 6.67$ feet then $d = 16.10$ feet.

Penny