| |||
| Math Central | Quandaries & Queries |
|
Question from Shuvo: The diagram shows a vertical cross-section of a container in the form of an inverted cone of height 60 cm and base radius 20 cm. The circular base is held horizontal and uppermost. Water is pursed into the container at a constant rate of 40 cm3/s. Show that, when the depth of water in the container is x cm, the volume of the water in the container is (πx^3)/27 cm3. |
Hi,
This is my diagram of what you described. All the lengths are in centimeters.
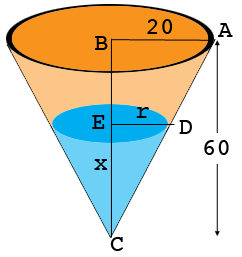
I let $r$ be the radius of the circular disk that forms the surface of the water.
Triangles $ABC$ and $DEC$ are similar so
\[\frac{|AB|}{|BC|} = \frac{|DE|}{|EC|}=\frac{r}{x}\]
But $|AB|$ is $\frac13$ of $|BC|$ so $r = \frac13 x.$
Write the equation for the volume $V$ of water in the cone. Use the relationship between $r$ and $x$ above to express $V$ in terms of $x.$
Penny
 |
||
| * Registered trade mark of Imperial Oil Limited. Used under license. | ||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.