Hi Tinashe,

The circumference of a circle is $\pi$ times the diameter so in your circle the circumference is $10 \times \pi.$

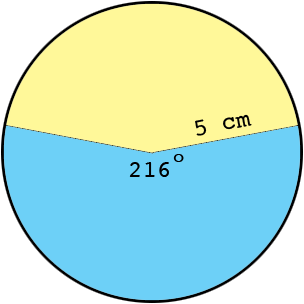
Thus the $216^o$ sector of this circle, shaded blue, is subtended by an arc of length

\[\frac{216}{360} \times 10 \times \pi \mbox{ centimeters}\]

If you roll up the blue sector in the diagram above to form a cone then the arc of length

\[\frac{216}{360} \times 10 \times \pi \mbox{ centimeters}\]

forms the circumference of the base circle of the cone.

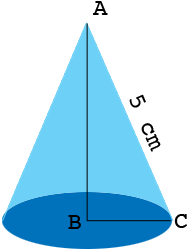
Use the formula for the circumference of a circle to find the radius, |BC|, of the base circle. Use the triangle ABC to determine the vertical angle.

Penny