Hi Tom,

I want to illustrate with small integers. I'm going to convert $\large \frac{3}{7}$ to decimal form. I do this with long division. I have omitted the decimal to make the formatting easier.

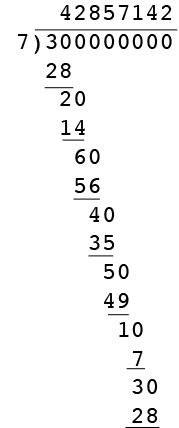
At each step after the first you divide 7 into ten times the remainder from the previous step. In this example I eventually get a remainder of 3, which is the numerator of the original fraction so the pattern repeats and

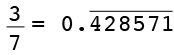
At each step of the division algorithm you have a divisor of 7 and a remainder which must be a nonnegative integer, less than 7, that is 0, 1, 2, 3, 4, 5 or 6.

Similarly suppose you want to convert the fraction, $\large \frac{n}{d},$ where $n$ and $d$ are positive integers, to a decimal using the long division algorithm . At each step in the algorithm you divide by $d$ and one of the $d$ possible remainders. If the remainder at any step os zero then the algorithm terminates and you have $\large \frac{n}{d}$ expresses with a finite number of decimal places. Otherwise in $d+1$ steps you must have the same remainder at least twice and the decimals repeat.

I hope this helps,
Penny