Hi,

This problem is an ancient problem in architecture and design, and has been studied by mathematicians from antiquity to the present.

Let's take a look at an example of two tubes (right circular cylinders, to be precise) of equal radius intersecting at an angle other than 90 degrees; let’s say 60 degrees, just to give a particular example.

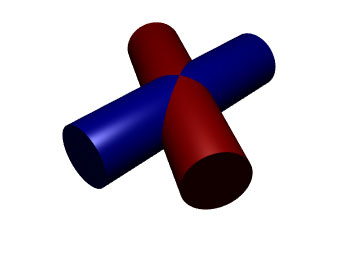
Note from the diagram that the figure (ignoring the colours, which are only there to help us make sense of the situation) has two vertical planes of mirror symmetry (and a third horizontal plane of mirror symmetry, which is not important in this discussion). The intersections of the tubes fall along one or the other of the planes of symmetry. Note that the two planes of symmetry are perpendicular to one another.

Using those planes as guides, we can figure out how to cut the tubes to join together. First, let’s say both tubes are hollow. We'll leave the blue tube intact, and cut the red tube. We make the first cut along a plane halfway between the axes. Since the axes are separated by 60 degrees in our example, the angle between the axis of the red tube and the cutting plane is 30 degrees. (It will always be half of the angle between the tubes.) Next, find the position halfway along the cut (which will identify the point where all four parts intersect in the above diagram) and make a second cut through that point at a 90 degree angle to the first cut. That gives you one red tube. The second red tube is identical to the first. If the tubes were infinitely thin, they would now fit together perfectly at the appropriate angle. Since they have some thickness, additional deformation of the red tubes may be required, or cutting material out of the blue tube.

If both tubes are solid, then you could perform the same procedure as above with both the red tubes and the blue tubes. (If you followed the exact same procedure with the blue tubes as with the red tubes, the blue tubes would end up being upside down, but that’s not a problem at all because they can just be turned over.) Then all four pieces can be assembled.

If cutting the blue tubes weakens the structure too much, then the red tubes could be cut according to the above instructions, and then I suppose it could be "hollowed out" by a cutting tool which would cut out a space for the blue tube.

I hope that answers your question.

Edward