Hi Ariel,

The expression

\[\mbox{ the area of a sector of a circle of radius r } is \frac12 r^2 \theta.\]

is valid if the angle is measured in radians.

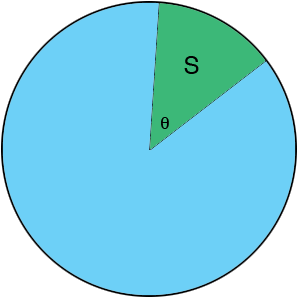
The diagram above is a circle of radius $r$ and a sector $S$ subtended by an angle of $\theta$ radians at the center of the circle. The area of the sector $S$ is a fraction of the area of the circle and the measure of the angle $\theta$ is a fraction of the measure of the angle subtending circle which is $2 \pi$ radians or $360^{o}.$ The symmetry of the circle implies that these two fractions are equal. That is

\[\frac{\mbox{area of the sector S}}{\mbox{area of the circle}} = \frac{\theta}{2 \pi},\]

or said slightly differently

\[\mbox{area of the sector S} = \frac{\theta}{2 \pi} \times \mbox{area of the circle} = \frac{\theta}{2 \pi} \times \pi r^2 = \frac12 r^2 \theta.\]

I hope this helps,
Penny