Hi,

I started a chain as Claude described starting with [0,1]. My chain was

[0,1][1,3][3,4][4,5][5,6][6,0][0,0][0,2][2,1][1,4][4,0][0,5][ 5,3][3,0]

I could continue as Claude describes to use the 28 dominos and my list and his are different. I am sure of this since in his list [0,4] is between [0,3] and [0,5] and in my list it is not.

Penny

We got a response

This answer supplied is not rigorous. Since the final line will have matching values at both ends, it can be considered to be circular (i.e. connect those ends to make a circle). Hence, for the completed sequence, any given tile is, in some sense, ALWAYS between any two other tiles -- you just have to go the correct direction (CW or CCW) to observe 'in between-ness." If you break the circle, you can make it so a tile is not between a particular pair, but that is not a new solution, that is just starting the line with a different tile.

- BHS

I am going to label four of the dominos, $A$ is [01], $B$ is [0,3], $C$ is [[04], and $D$ is [05]. If you complete Claude's solution and place the dominos clockwise on a circle then you get

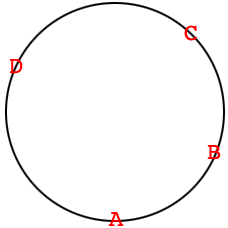
with the remaining dominos in the appropriate positions. Notice that if you start at $A$ and go around the circle either clockwise or counterclockwise, $C$ is between $B$ and $D.$

If you complete my solution and place the dominos clockwise on a circle then you get

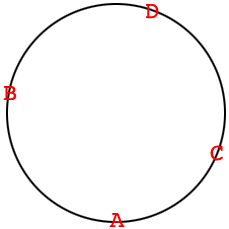
Hence the two solutions are different.

Penny