Hi Darren,

I'm going to change the problem to two dimensions rather than three but increase the size of the array.

How many squares of different sizes (eg. 1x1, 2x2, 3x3, 4x4) are there in total in a 4x4 square?

Hopefully you will be able to modify my method to solve your three dimensional problem. Here is my 4x4 square.

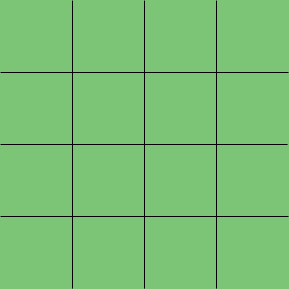
There is only one 4x4 square. What about 3x3 squares? I am going to start with 3x3 squares with their tops along the top of the 4x4 square. here is one.

I can shift it one square to the right to get

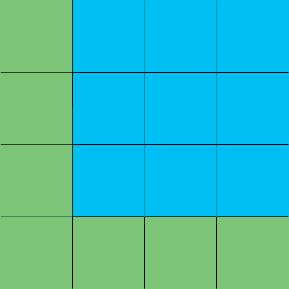
I can shift each 3x3 blue square down one square to get two more 3x3 squares inside the 4x4 square

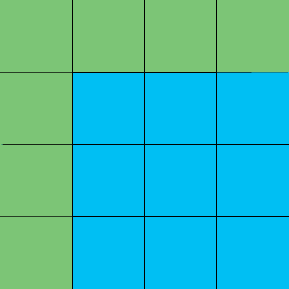
Hence there are $2 \times 2 = 4$ 3x3 squares in the 4x4 square. What about 2x2 squares? Again start by placing 2x2 squares with top edges along the top of the 4x4 square.

This blue 2x2 square can be shifted one and then two units to the right to obtain

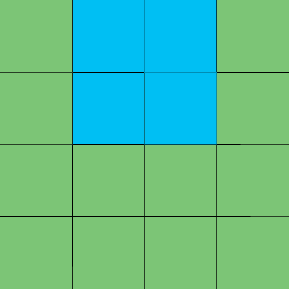
Hence there are 3 2x2 squares along the top. Each of these can be shifted down 1 and then 2 squares to produce $3 \times 3 = 9$ 2x2 squares inside the 4x4 square. Finally just by counting there are $4 \times 4 = 16$ 1x1 squares.

Hence the answer to my question is $1 + 4 + 9 + 16$ squares.

Can you modify my argument to solve your original question or maybe even a 4x4x4 cube?

Write back if you need further assistance,
Penny