Hi Don,

How about $x^2 + y^2 = 0?$ $x = 0, y = 0$ is a solution, but is there another?

Rewrite the equation as $y^2 = -x^{2}. If $x \neq 0$ then $x^2$ is positive and hence $-x^2$ is negative but $y^2$ can't be negative. Hence there is no solution with $x \neq 0.$ Similarly there is no solution with $y \neq 0.$ Hence $x = 0, y = 0$ is the only solution of $x^2 + y^2 = 0.$

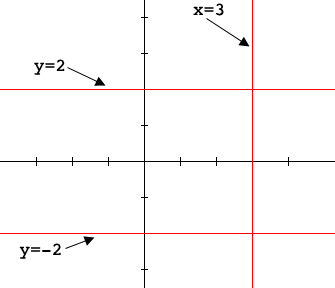
Now look at $xy^2 - 3y^2 - 4x + 12 = 0.$ This can be rewritten as $y^2 (x - 3) -4( x - 3) = 0$ or $(x-3)(y^2 - 4) = 0.$ Thus the product of the two numbers $x - 3$ and $y^2 - 4$ is zero and hence at least one of them must be zero. Hence the solution of $y^2 (x - 3) -4( x - 3) = 0$ is $\left\{ (x,y): x=3, y=2 \mbox{ or } y = -2 \right\}. $ Geometrically that's all the points on the lines $x = 3, y = -2$ and $y = -2.$

Penny