Hi Guy,

The size of the hole depends on the thickness of the board. I am going to do this where the angle at which the tube meets the board is $d^o$ and the thickness of the board is $t$ inches, and when I'm done set $d = 45^{o}.$

Here is my diagram.

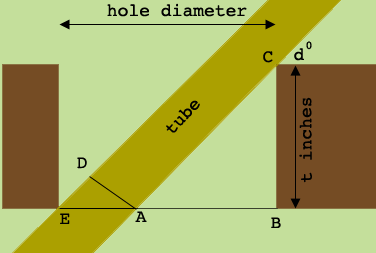
Let the distance from $A$ to $B$ be $y$ inches and the distance from $E$ to $A$ be $x$ inches then the diameter of the hole to be drilled is $x + y$ inches.

The measure of the angle $CAB$ is $d^o$ and hence

\[\tan(d^o) = \frac{t}{y} \mbox { or } y = \frac{t}{\tan(d^o)}.\]

Since the sides of the tube are parallel the measure of the angle $DEA$ is $d^{o}.$ The distance from $D$ to $A$ is 5/8 inches and hence

\[\sin(d^o) = \frac{5/8}{x} \mbox{ or } x = \frac{5/8}{\sin(d^0)}.\]

When $d^o = 45^o$ we have $\tan(d^o) = 1$ and hence $y = t \mbox{ inches}$ and $\sin(d^o) = \large \frac{1}{\sqrt{2}}$ so

\[x = \frac{5}{8} \times \sqrt {2} = 0.884 \mbox{ inches.} \mbox{ which is approximately 7/8 of an inch.}\]

I hope this helps,
Harley